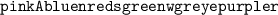

★ 1st let's know what is the given figure is and it's related concepts for solving !
- ➣ Given Triangle is a right angled triangle
- ➣ It is having 3sides let's know what are the name of these sides
- ➣ 1st AB is know as hypotenuse
- ➣ 2nd AC and is called Base of the triangle
- ➣ 3rd BC whích is know as perpendicular of the triangle
- ➣ Hypotenuse(H):-The side of a right triangle opposite the right angle.
- ➣ Perpendicular(P):- Exactly upright; extending in a straight line.
- ➣ Base(B):- it also known as the side opposite to hypotenuse
- ➣Perpendicular and base are know as the leg of right angled triangle
- ➣ We can easily find length of one missing side by using a theorem name as "Pythagorean theorem"
- ➣ Pythagorean theorem :- A mathematical theorem which states that the square of the length of the hypotenuse of a right triangle is equal to the sum of the squares of those of the two other sides
- ★ Note :- The Pythagorean theorem only applies to right triangles.

★ Writing this theorem mathematically ★

★ Here ★
- ➣ Base (AC)= 8cm
- ➣ Hypotenuse (BA)= 13cm

✝ Assumption ✝
- ➣ let perpendicular/length ( BC ) = "x"
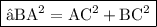

✝ let's substitute values ✝
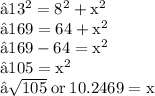

Hence length (BC) in the given triangle is of


Hope it helps !