Answer:
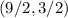
Step-by-step explanation:
We have the equation:
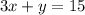
Which is equivalent to 15 among all pairs of (x, y).
We want to find the pair of solutions (x, y) such that:
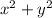
Is minimum.
Note that our given equation is a line.
And the equation x²+y² is a circle centered on the origin.
In other words, we want to find the radius of the circle such that it is tangent to our line at 3x+y=15.
It must be tangent because this guarantees that it is the smallest value of x²+y².
It's good if we have a visual of this. I've graphed the given linear equation. Please refer to it.
If you remember in geometry, in order for the radius to be tangent to a line, the radius must be perpendicular to our line.
So, let's find the perpendicular equation to our line. Our original equation is:
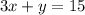
Subtract 3x from both sides:
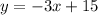
So, the slope of our original equation is -3.
This means that the slope of our perpendicular line must be the negative reciprocal of -3. Namely, it is 1/3.
And since our circle is centered on the origin, this line will go through the origin. Therefore, our perpendicular equation is:
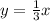
Graphing this will yield (please refer to the second graph):
Therefore, the intersection between our old and new line is at (4.5, 1.5).
Therefore, the (x, y) value that grants the minimum sum is 9/2 and 3/2.
We can check this by substituting them into our second equation. This yields:

Square and add:
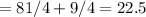
Note that 22.5 is the radius squared.
Graphing this gives us (please refer to the third graph):
We can see that it is indeed tangent to our line. And it is the lowest value of P that does so.
So, our answer is x=9/2 and y=3/2.