Question

A quadrilateral WXYZ has vertices W(3, −5), X(1, −3), Y(−1, −5), and Z(1,−7). What are the vertices of r(90, O)(WXYZ)?

Answer 1

Given:

A quadrilateral WXYZ has vertices W(3, −5), X(1, −3), Y(−1, −5), and Z(1,−7).

Rule of rotation is
`r_((90^\circ, O))(WXYZ)`.

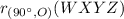To find:

The vertices after rotation.

Solution:

We know that,
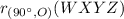`r_((90^\circ, O))(WXYZ)` means 90 degrees counterclockwise rotation around the origin.

So, the rule of rotation is defined as

`(x,y)\to (-y,x)`

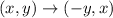
Using this rule, we get

`W(3,-5)\to W'(5,3)`

`X(1,-3)\to X'(3,1)`

`Y(-1,-5)\to Y'(5,-1)`

`Z(1,-7)\to Z'(7,1)`

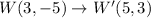
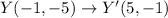
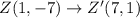
Therefore, the required vertices after rotation are W'(5,3), X'(3,1),Y'(5,-1) and Z'(7,1).