Answer:
The system of equations is y = -2, x - 2y = 6 ⇒ (a)
Explanation:
Let us revise some facts about the linear equation
The form of the linear equation is y = m x + b, where m is the slope of the line and b is the y-intercept [the line intersect the y-axis at point (0, b)]
The equation of any horizontal line is y = b
The equation of any vertical line is x = a, where (a, 0) is the x-intercept
Now let us study the given graph
→ Blue line
∵ The blue line is a horizontal line
∴ Its equation is y = b
∵ b is the y-coordinate of the y-intercept
→ The line intersects the y-axis at point (0, -2) which means b = -2
∴ b = -2
∴ The equation of the blue line is y = -2
We have two answers only with the equation y = -2, a and b, so the answer must be one of them. Let us find the equation of the red line to decide which one is the answer.
→ Red line
∵ The equation of the line is y = m x + b
∵ The read line intersects the y-axis at point (0, -3)
∴ b = -3
∴ y = m x + (-3)
∴ y = mx - 3
→ To find m substitute x and y by the coordinates of any point on the line
∵ Point (6, 0) lies on the line
∴ x = 6 and y = 0
∵ 0 = m(6) - 3
∴ 0 = 6m - 3
→ Add 3 to sides
∴ 0 + 3 = 6m - 3 + 3
∴ 3 = 6m
→ Divide both sides by 6 to find m
∴
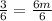
∴
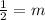
→ Substitute the value of m in the equation above
∴ y =
 x - 3
x - 3
→ Let us put x and y on one side and the number on the other
side by subtracting y and add 3 to both sides
∵ y - y + 3 =
 x - 3 + 3 - y
x - 3 + 3 - y
∴ 3 =
 x - y
x - y
→ Multiply both sides by 2
∴ 2(3) = 2(
 x) - 2(y)
x) - 2(y)
∴ 6 = x - 2y
→ Switch the two sides
∴ x - 2y = 6
∴ The equation of the red line is x - 2y = 6
∵ The equations of the blue line and the red line are in answer a
∴ The system of equations is y = -2, x - 2y = 6
Note: you can use the point of intersection of the lines on the graph (2, -2) and substitute its coordinates in each answer to find which answer will satisfy that the two sides in each equation are equal