Question

The maximum speed with which you can throw a stone is about 20 m/s. Can you hit a window 45 m away horizontally and 10 m up from the point where the stone leaves your hand? What is the maximum height of a window you can hit at this distance?

Answer 1

y = 17 m

Step-by-step explanation:

For this projectile launch exercise, let's write the equation of position

x = v₀ₓ t

y =
`v_(oy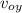)` t - ½ g t²

let's substitute

45 = v₀ cos θ t

10 = v₀ sin θ t - ½ 9.8 t²

the maximum height the ball can reach where the vertical velocity is zero

v_{y} = v_{oy} - gt

0 = v₀ sin θ - gt

0 = v₀ sin θ - 9.8 t

Let's write our system of equations

45 = v₀ cos θ t

10 = v₀ sin θ t - ½ 9.8 t²

0 = v₀ sin θ - 9.8 t

We have a system of three equations with three unknowns for which it can be solved.

Let's use the last two

v₀ sin θ = 9.8 t

we substitute

10 = (9.8 t) t - ½ 9.8 t2

10 = ½ 9.8 t2

10 = 4.9 t2

t = √ (10 / 4.9)

t = 1,429 s

Now let's use the first equation and the last one

45 = v₀ cos θ t

0 = v₀ sin θ - 9.8 t

9.8 t = v₀ sin θ

45 / t = v₀ cos θ

we divide

9.8t / (45 / t) = tan θ

tan θ = 9.8 t² / 45

θ = tan⁻¹ ( 9.8 t² / 45 )

θ = tan⁻¹ (0.4447)

θ = 24º

Now we can calculate the maximum height

v_y² =
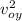`v_(oy)^2` - 2 g y

vy = 0

y = v_{oy}^2 / 2g

y = (20 sin 24)²/2 9.8

y = 3,376 m

the other angle that gives the same result is

θ‘= 90 - θ

θ' = 90 -24

θ'= 66'

for this angle the maximum height is

y = v_{oy}^2 / 2g

y = (20 sin 66)²/2 9.8

y = 17 m

thisis the correct