Question

I've done every problem I only need with the help this problem

Answer 1

Answers:

`\displaystyle \lim_(x \to 2^(+)) f(x) = 1\\\\\displaystyle \lim_(x \to 2^(-)) f(x) = 1\\`

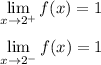
Both result in the same limit value. This allows us to say
`\displaystyle \lim_(x \to 2) f(x) = 1` without the plus or minus over the 2.

The left and right hand limits may not always match like this.

==================================================

Step-by-step explanation:

The notation
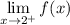`\displaystyle \lim_(x \to 2^(+)) f(x)` means that we are approaching x = 2 from the right hand side. This is from the positive direction. So we start at say x = 3 and move to x = 2.5 then to x = 2.1 then to x = 2.01 and so on.

Because we started with values x > 2, we will use the third definition of the piecewise function

if x > 2, then f(x) = 3x-5

Plug in x = 2 to get

f(x) = 3x-5

f(2) = 3(2)-5

f(2) = 6-5

f(2) = 1

This shows
`\displaystyle \lim_(x \to 2^(+)) f(x) = 1`

-----------------------------

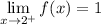
For the other limit, we're approaching x = 2 from the negative side. So we could start at say x = 0, then move to x = 1, then to x = 1.5 then to x = 1.9 then to x = 1.99, and so on.

We're using x values such that x < 2 now.

So we'll be using the first definition of the piecewise function

If x < 2, then f(x) = x^2 - 3

f(x) = x^2-3

f(2) = 2^2-3

f(2) = 4-3

f(2) = 1

We end up with
`\displaystyle \lim_(x \to 2^(-)) f(x) = 1`

---------------------------------

Both right hand limit and left hand limit result in the same value

Because
`\displaystyle \lim_(x \to 2^(+)) f(x) = \displaystyle \lim_(x \to 2^(-)) f(x) = 1`

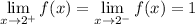
We can shorten that to
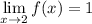`\displaystyle \lim_{x \to 2^{}} f(x) = 1` meaning we can approach x = 2 from either direction to arrive at the same limiting value.

A thing to notice is that f(2) is not equal to 1. Instead the second line of the piecewise function says f(2) = 3.

The fact that the limit as x approaches 2 and f(2) don't agree means this function is not continuous at x = 2.

The graph shows this. We have a removable discontinuity where we effectively picked the point off the graph and move it upward.

See the diagram below.