Question

Using Slopes of Parallel Lines Quick Check

Item 1
A quadrilateral ABCD has vertices A at (0,2), B at (2,6), C at (9,6), and D at (7,2). Are the opposite sides of this
quadrilateral parallel? (1 point)
Item 2
O Yes. AB is parallel to CD, but AD is not parallel to BC
Item 3
Item 4
O Yes. AB is parallel to CD and AD is parallel to BC
Item 5
O NO AD is parallel to BC but AB is not parallel to CD
O NO AB is parallel to CD, and AD is parallel to BC

Answer 1

The answer is (B) ⇒ Yes. AB is parallel to CD and AD is parallel to BC

Explanation:

There is an important fact about the parallel lines:

• Parallel lines have equal slopes

The rule of the slope of a line is:

• 
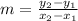  `m=(y_(2)-y_(1) )/(x_(2)-x_(1))`, where
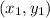  `(x_(1),y_(1))` and
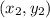  `(x_(2),y_(2))` are two points on the line

Let us use the fact and the rule to solve the question

∵ ABCD is a quadrilateral

∵ A = (0, 2) , B = (2, 6), C = (9, 6), D = (7, 2)

∵ The opposite sides are AB, CD and AD, BC

Find the slopes of the four sides to check the parallel sides

∵
`m_(AB)=(6-2)/(2-0)=(4)/(2)=2`

∵
`m_(CD)=(2-6)/(7-9)=(-4)/(-2)=2`

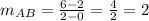
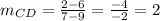
∵ The slope of AB = The slope of CD

∴ AB // CD

∵
`m_(AD)=(2-2)/(7-0)=(0)/(7)=0`

∵
`m_(BC)=(6-6)/(9-2)=(0)/(7)=0`

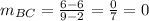
∵ The slope of AB = The slope of CD

∴ AD // BC

The correct answer is:

Yes. AB is parallel to CD and AD is parallel to BC ⇒ (B)