Question

4tanA%1-tan^4A=tan2A+sin2A​

Answer 1

See prove of the identity below

Explanation:

Recall that the following difference can be factored out as:

`(1-tan^4(A)) = (1+tan^2(A)) *(1-tan^2(A))`

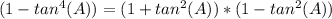
Now we look at the right side of the equal sign, and recall the identity that relates the sine of a double angle 2A with an expression in terms of the tan(A):

`sin(2A) = (2\,tan(A))/(1+tan^2(A))`

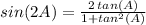
and similarly, the tangent of the double angle "2A" can be written as:

`tan (2A) = (2*tan(A))/(1-tan^2(A))`

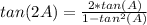
We can then combine the two expressions on the right using the common denominator:
`(1-tan^4(A)) = (1+tan^2(A)) *(1-tan^2(A))`:

`tan(2A) +sin(2A)=(2*tan(A)*(1+tan^2(A)))/(1-tan^4(A)) +(2*tan(A)*(1-tan^2(A)))/(1-tan^4(A)) \\=(2*tan(A)+2*tan(A))/(1-tan^4(A)) =(4*tan(A))/(1-tan^4(A))`

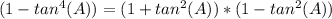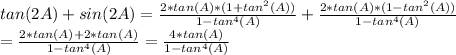
And we have proved the identity since the right hand side becomes exactly equal to the left hand side of the equal sign.