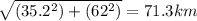Question

A car travels 32 km due north and then 46 km in a direction 40 degrees west of north. Find the magnitude of the cars resultant vector nearest tenth

Answer 1

Explanation:

In order to find the magnitude of the car's final displacement (resultant displacement vector), we need the x and y components of each part of the car's journey. We will call them vector A and vector B. The info for the vectors is as follows:

A: magnitude 32 at an angle of 90.0

B: magnitude 46 at an angle of 40.0

The x components are found in the formula

A(x) = magA*cos(angle)

For A(x):

A(x) : 32cos(90.0) = 0.0 and

For B(x) : 46cos(40.0) = 35.2

For A(y): 32sin(90.0) = 32 and

For B(y): 46sin(40.0) = 3.0 × 10¹

To get the x components of the final vector, add the x components of A and B together:

C(x) : 0.0

35.2

35.2

To get the y components of the final vector, add the y components of A and B together:

C(y) : 32

30

62

Now to get the magnitude, throw it into the magnitude formula, which is identical to Pythagorean's theorem:

C(mag) =
`√((35.2^2)+(62^2))=71.3 km`