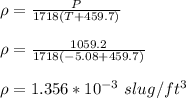Question

At a particular sea level location at a particular time the atmospheric pressure is 14.8 lbs/in^2 and the temperature is 80 degrees F. Estimate the temp, pressure , and air density at an altitude of 8,000ft? 18,000 ft? Note: You must modify the standard atmosphere model using the given values for sea level air pressure and temperature

Answer 1

(a) At 8,000 ft :

The air temperature is 30.52 °F

The air pressure is 1574 lbs/ft²

The air density is 1.869 x 10⁻³ slug/ft³

(b) At 18,000 ft :

The air temperature is -5.08 °F

The air pressure is 1059.2 lbs/ft²

The air density is 1.356 x 10⁻³ slug/ft³

Explanation:

Given;

pressure at sea level, P₀ = 14.8 PSI

temperature, T' = 80 °F

At 8,000 ft (m) altitude

for altitude h, less than 36,152 ft, the following model is used to modify temperature and pressure;

T = 59 - 0.00356h

T = 59 - 0.00356(8,000)

T = 30.52 °F

The pressure is calculated as;

`P = 2116[(T+459.7)/(518.6) ]^(5.256)\\\\P = 2116[(30.52+459.7)/(518.6) ]^(5.256)\\\\P = 1574.2 \ lbs/ft^2`

The density is given by;

`\rho = (P)/(1718*(T+459.7))\\\\\rho = (1574.2)/(1718*(30.52+459.7))\\\\\rho = 1.869*10^(-3) \ slug/ft^3`

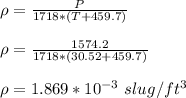
For 18,000 ft

T = 59 - 0.00356h

T = 59 - 0.00356(18,000)

T = -5.08 °F

The pressure is calculated as;

`P = 2116[(T+459.7)/(518.6) ]^(5.256)\\\\P = 2116[(-5.08+459.7)/(518.6) ]^(5.256)\\\\P = 1059.2 \ lbs/ft^2`

The density is given by;

`\rho = (P)/(1718(T+459.7)) \\\\\rho = (1059.2)/(1718(-5.08+459.7))\\\\ \rho = 1.356*10^(-3) \ slug/ft^3`