Answer:
For the control experiment:
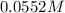 of aqueous solution of erioglaucine has absorbance of
of aqueous solution of erioglaucine has absorbance of
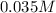
From Lambert-Beer's law we know:
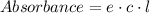
Here; e is the molar absorptivity coefficient of erioglaucine
l = length of cuvette in which the solution is taken =
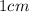
A sorbance by the erioglaucine = total absorbance - absorbance by distilled

So; by putting the values in the above equation; we get:
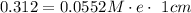
So;
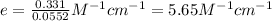
The molar absorptivity coefficient of erioglaucine is
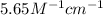
The absorbance of erioglaucine in distilled water (contaminated with metal ions) is:
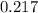
The absorbance of distilled water is
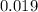
So; absorbance of erioglaucine itself is :
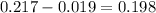
Again using Lambert Beer law; we get:
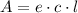
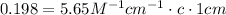
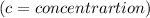
c = 0.198/5.65 M = 0.035 M
The concentration of the erioglaucine is
Step-by-step explanation: