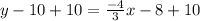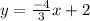Question

Jacob is using coordinate system to design a rhombus-shaped building. Side LaTeX: \frac{ }{AB}A B passes through point (6, 6) and is perpendicular to the graph of LaTeX: y=\frac{3}{4}x-11y = 3 4 x − 11. Side LaTeX: \frac{ }{CD}C D is parallel to side LaTeX: \frac{ }{AB} and passes through point (−6, 10). What is the equation in slope-intercept form of the line that includes side LaTeX: \frac{ }{CD}

Answer 1

`y= (-4)/(3)x +2`

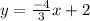
Explanation:

Given

`AB = (6,6)`

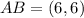
perpendicular to

`y = (3)/(4)x - 11`

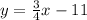
CD parallel to AB

CD passes through (-6,10)

Required

Determine the slope-intercept form of line CD

First, we need to determine the slope of AB

For
`y = (3)/(4)x - 11`

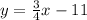
Slope,
`m_1 = (3)/(4)`

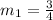
Represent slope of AB with m2

Since both are perpendicular:

`m_2 = -1/m_1`

`m_2 = -1/(3)/(4)`

`m_2 = -1 * (4)/(3)`

`m_2 = (-4)/(3)`

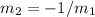
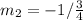
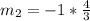
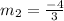
To determine the equation of CD, we need to determine its slope:

Since CD is parallel to AB, then

`m = m_2 = (-4)/(3)`

The slope intercept form of CD is as follows;

`y - y_1 = m(x - x_1)`

Where:

`(x_1,y_1) = (-6,10)`

`y - y_1 = m(x - x_1)`

`y - 10 = (-4)/(3)(x - (-6))`

`y - 10 = (-4)/(3)(x +6)`

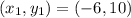
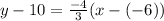
Open Bracket

`y - 10 = (-4)/(3)x +(-4)/(3) * 6`

`y - 10 = (-4)/(3)x -4 * 2`

`y - 10 = (-4)/(3)x -8`

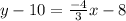
Add 10 to both sides

`y - 10 + 10= (-4)/(3)x -8 + 10`

`y= (-4)/(3)x +2`