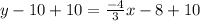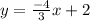Answer:
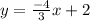
Explanation:
Given
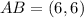
perpendicular to
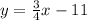
CD parallel to AB
CD passes through (-6,10)
Required
Determine the slope-intercept form of line CD
First, we need to determine the slope of AB
For
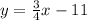
Slope,
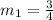
Represent slope of AB with m2
Since both are perpendicular:
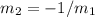
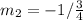
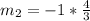
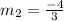
To determine the equation of CD, we need to determine its slope:
Since CD is parallel to AB, then
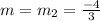
The slope intercept form of CD is as follows;
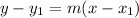
Where:
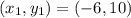
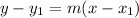
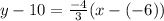
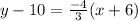
Open Bracket
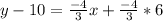
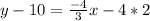
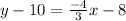
Add 10 to both sides