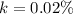Question

How do you interpret the estimated value of coefficient of EDU in the following equation:

ln(SALARY)= 1 + 0.02ln(EDU)

where SALARY is annual salary (in thousands) and EDU is years of education?

a.
we predict that 1 year increase in years of education leads to $2000 increase in salary

b.
we predict that 1% increase in years of education leads to 2% increase in salary

c.
we predict that 1 year increase in years of education leads to 2% increase in salary

d.
we predict that 1% increase in years of education leads to 0.02% increase in salary

Answer 1

The correct option is d

Explanation:

From the question we are told that

The equation is
`ln (SALARY) = 1 + 0.02 ln(EDU)`

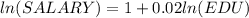
generally

`ln (e) = 1`

=>
`ln (SALARY) = ln (e) + 0.02 ln(EDU)`

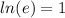
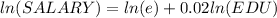
Apply log rules

=>
`ln (SALARY) = ln[ e(EDU)^(0.02) ]`

=>
`SALARY = e(EDU)^(0.02)`

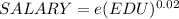
When EDU is increase by 1% we have that

`(1)/(100) * EDU + EDU`

=>
`1.01 EDU`

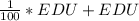
So the new SALARY will now be

`SALARY'' = e(1.01EDU)^(0.02)`

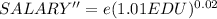
The ratio by which the new SALARY will increase is obtain by dividing the value of new SALARY (SALARY'' ) with that of the former SALARY (SALARY) and this mathematically represented as

`(SALARY'' )/(SALARY) = (e*1.01 (EDU)^(0.02))/(e (EDU)^(0.02))`

=>
`(SALARY '')/(SALARY) = 1.0002`

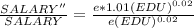
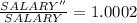
Generally the percentage increase of salary is mathematically evaluated as

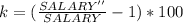
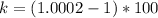
`k= ((SALARY'')/(SALARY) - 1 ) * 100`

=>
`k= (1.0002 - 1 ) * 100`

=>
`k= 0.02 \%`