Question

A square has sides with lengths of (x − 1) units. A rectangle has a length of x units and a width of (x − 2) units. Which statements about the situation are true? Select all that apply. A The value of x must be greater than 2. B The difference in the areas is 2x−1. C The area of the square is (x2 − 1) square units. D The area of the rectangle is (x2 − 2x) square units. E The area of the square is greater than the area of the rectangle.

Answer 1

A, D, E

Explanation:

AREA OF SQUARE

`(x - 1)(x - 1) = x^2 - 2x + 1`

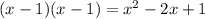
AREA OF RECTANGLE

`x(x - 2) = x^2 - 2x`

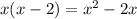
Using this we know that the difference is 1, so B is incorrect. We also know that D and E are correct because we solved for the area. C is also wrong, by the same reasoning. Now, all we need to see is if A is right. Plug in x = 2.

`(2)^2 - 2(2) + 1 \\= 4 - 4 + 1 \\= 1`

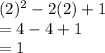
Because the area of the square is a square unit larger than the rectangle, the rectangle would have an area of 0, which is impossible, so A is correct.