Question

1. A line goes through the points (7, 3) and (–1, 5). Write the equation of the line in point-slope form. Show your work for full credit. (How did you go from those two points to having the equation in point-slope form?)

Answer 1

A line goes through the points (7, 3) and (–1, 5).

To find:

The equation of the line in point-slope form.

Solution:

The lines goes through the points (7, 3) and (–1, 5). So, slope of line is

`m=(y_2-y_1)/(x_2-x_1)`

`m=(5-3)/(-1-7)`

`m=(2)/(-8)`

`m=-(1)/(4)`

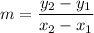
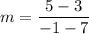
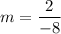
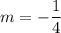
So, slope of the line is
`m=-(1)/(4)`.

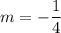Now,

Point slope form of a line is

`y-y_1=m(x-x_1)`

where, m is slope and
`(x_1,y_1)` is any point on the line.

If slope of line is
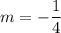`m=-(1)/(4)` and the point is (7, 3), then point slope form of line is

`y-3=-(1)/(4)(x-7)`

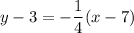
If slope of line is
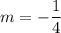`m=-(1)/(4)` and the point is (-1, 5), then point slope form of line is

`y-5=-(1)/(4)(x-(-1))`

Therefore, the required equations are either
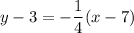`y-3=-(1)/(4)(x-7)` or
`y-5=-(1)/(4)(x-(-1))`.