Answer:
A line goes through the points (7, 3) and (–1, 5).
To find:
The equation of the line in point-slope form.
Solution:
The lines goes through the points (7, 3) and (–1, 5). So, slope of line is
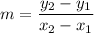
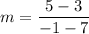
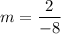
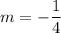
So, slope of the line is
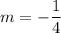 .
.
Now,
Point slope form of a line is
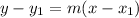
where, m is slope and
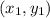 is any point on the line.
is any point on the line.
If slope of line is
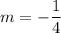 and the point is (7, 3), then point slope form of line is
and the point is (7, 3), then point slope form of line is
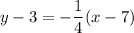
If slope of line is
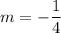 and the point is (-1, 5), then point slope form of line is
and the point is (-1, 5), then point slope form of line is
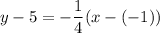
Therefore, the required equations are either
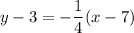 or
or
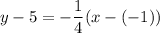 .
.