x - the larger integer (x>0)
x-1 - the smaller integer (the difference between two consecutive integers is always 1)
The product of two consecutive positive integers is 1,332
so:
x•(x -1 ) = 1332
x² - x = 1332
x² - x - 1332 = 0 ⇒ a = 1, b = -1, c = -1332
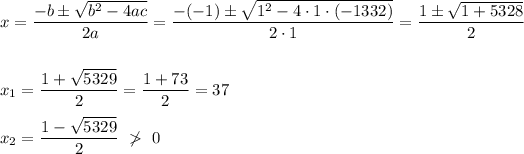
x = 37