Answer:
1) B
2) C
Explanation:
Question 1)
We have the function:

Note that this is in the standard quadratic form:

Unfortunately, since this isn't in vertex form, we need to do a bit more work for our vertex.
Remember that we can find our vertex using the following formulas:
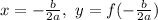
Let's label our coefficients. Our a is 2, b is 24, and c is -16.
Let's find our vertex. Substitute 24 for b and 2 for a. This yields:
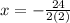
Multiply:

Divide:

So, the x-coordinate of our vertex is -6.
Now, to find the y-coordinate, we simply need to substitute x for our equation. We have:

Substitute -6 for x:

Evaluate. Square:
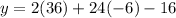
Multiply:
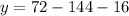
Subtract. So, the y-coordinate of our vertex is:
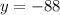
So, our vertex point is (-6, -88).
Remember that the axis of symmetry is the same as the x-coordinate of our vertex. So, our axis of symmetry is at x=-6.
Therefore, our answer is B.
Question 2)
We have the equation:
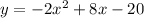
Again, we can use the above formula. Let's label of coefficients.
Our a is -2, b is 8, and c is -20.
So, let's find the x-coordinate of our vertex:
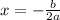
Substitute 8 for b and -2 for a:
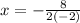
Multiply:
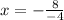
Divide. The negatives cancel. So, our x-coordinate is:

Now, substitute this back into the equation to find the y-coordinate:

Square:
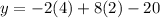
Multiply:
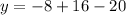
Add:
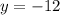
Therefore, our vertex is (2, -12).
And the axis of symmetry is at x=2.
Our answer is C.
And we're done!