Question

Need 2 more. 50 points!

Please show work, Thanks! :)

Answer 1

1) C

2) C

Explanation:

Question 1)

We want a parabola that has the vertex (-8, -7) and also passes through the point (-7, -4).

So, we can use the vertex form. Remember that the vertex form is:

`y=a(x-h)^2+k`

Where a is our leading co-efficient and (h, k) is our vertex.

We know that our vertex is (-8, -7). So, substitute this into the equation:

`y=a(x-(-8))^2+(-7)`

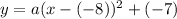
Simplify:

`y=a(x+8)^2-7`

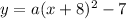
Now, we need to determine the value of our a. To do so, we can use the point the problem had given us. We know that the graph passes through (-7, -4).

So, when x is -7, y is -4. Substitute -7 for x and -4 for y:

`(-4)=a((-7)+8)^2-7`

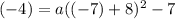
Solve for a. Add within the parentheses:

`-4=a(1)^2-7`

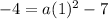
Square:

`-4=a-7`

Add 7 to both sides. Therefore, the value of a is:

`a=3`

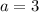
So, our entire equation in vertex form is:

`y=3(x+8)^2-7`

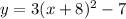
Our answer is C.

Question 2)

We are given a graph and are asked to find the equation of the graph.

Again, let's use the vertex form. From the graph, we can see that the vertex is at (-2, 2). Let's substitute this into our vertex equation:

`y=a(x-(-2))^2+2`

Simplify:

`y=a(x+2)^2+2`

Again, we need to find the value of a.

Notice that the graph crosses the point (-1, 5).

So, let's substitute -1 for x and 5 for y. This yields:

`5=a((-1)+2)^2+2`

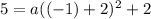
Solve for a. Add within the parentheses.

`5=a(1)^2+2`

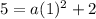
Square:

`5=a+2`

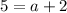
Subtract 2 from both sides. So, the value of a is:

`a=3`

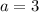
Therefore, our entire equation is:

`y=3(x+2)^2-2`

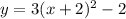
Our answer is C.

And we're done!