Question

Suppose that a large mixing tank initially holds 500 gallons of water in which 50 pounds of salt have been dissolved. Another brine solution is pumped into the tank at a rate of 3 gal/min, and when the solution is well stirred, it is then pumped out at a slower rate of 2 gal/min. If the concentration of the solution entering is 4 lb/gal, determine a differential equation for the amount of salt A(t) in the tank at time

t > 0.

(Use A for

A(t).)

I got 6-(2A/t+500) Im not sure if the 6 is right the rate part since on another one the concentration entering was 2 lb/gal not 4 lb/gal

Answer 1

The differential equation for the amount of salt A(t) in the tank at a time t > 0 is
`(dA)/(dt)=12 - (2A(t))/(500+t)`.

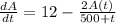Explanation:

We are given that a large mixing tank initially holds 500 gallons of water in which 50 pounds of salt have been dissolved. Another brine solution is pumped into the tank at a rate of 3 gal/min, and when the solution is well stirred, it is then pumped out at a slower rate of 2 gal/min.

The concentration of the solution entering is 4 lb/gal.

Firstly, as we know that the rate of change in the amount of salt with respect to time is given by;

`(dA)/(dt)= \text{R}_i_n - \text{R}_o_u_t`

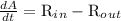
where,
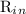`\text{R}_i_n` = concentration of salt in the inflow
`*` input rate of brine solution

and
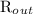`\text{R}_o_u_t` = concentration of salt in the outflow
`*` outflow rate of brine solution

So,
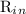`\text{R}_i_n` = 4 lb/gal
`*` 3 gal/min = 12 lb/gal

Now, the rate of accumulation = Rate of input of solution - Rate of output of solution

= 3 gal/min - 2 gal/min

= 1 gal/min.

It is stated that a large mixing tank initially holds 500 gallons of water, so after t minutes it will hold (500 + t) gallons in the tank.

So,
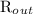`\text{R}_o_u_t` = concentration of salt in the outflow
`*` outflow rate of brine solution

=
`(A(t))/(500+t) \text{ lb/gal } * 2 \text{ gal/min}` =
`(2A(t))/(500+t) \text{ lb/min }`

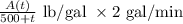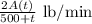
Now, the differential equation for the amount of salt A(t) in the tank at a time t > 0 is given by;

=
`(dA)/(dt)=12\text{ lb/min } - (2A(t))/(500+t) \text{ lb/min }`

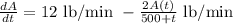
or
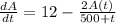`(dA)/(dt)=12 - (2A(t))/(500+t)`.