Answer:
The speed of the ball is 10 meters per second.
Step-by-step explanation:
The fact that ball rotates uniformly means that speed of the ball is constant and resulting acceleration is centripetal, which means that external horizontal force exerted on the ball goes towards the center of rotation. We can estimate the speed of the ball by this equation of equilibrium:
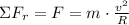 (Eq. 1)
(Eq. 1)
Where:
 - External force exerted on the ball, measured in newtons.
- External force exerted on the ball, measured in newtons.
 - Mass of the ball, measured in kilograms.
- Mass of the ball, measured in kilograms.
 - Linear rotation speed, measured in meters per second.
- Linear rotation speed, measured in meters per second.
 - Radius of rotation, measured in meters.
- Radius of rotation, measured in meters.
We clear the linear speed in (Eq. 1):
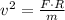
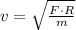
If we know that
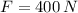 ,
,
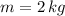 and
and
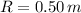 , the speed of the ball is:
, the speed of the ball is:
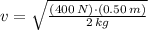
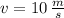
The speed of the ball is 10 meters per second.