Question

Nana has a water purifier that filters \dfrac13 3 1 ​ start fraction, 1, divided by, 3, end fraction of the contaminants each hour. She used it to purify water that had \dfrac12 2 1 ​ start fraction, 1, divided by, 2, end fraction kilogram of contaminants. Write a function that gives the remaining amount of contaminants in kilograms, C(t)C(t)C, left parenthesis, t, right parenthesis, ttt hours after Nana started purifying the water.

Answer 1

`(1)/(2) ((2)/(3) )^t`

Explanation:

It's correct on Khan.

Answer 2

Given:

Nana has a water purifier that filters
`(1)/(3)` of the contaminants each hour.

Water has contaminants =
`(1)/(2)`

To find:

The function that gives the remaining amount of contaminants in kilograms, C(t), t hours after Nana started purifying the water.

Solution:

Let C(t) be the remaining amount of contaminants in kilograms after t hours.

Initial amount of contaminants =
`(1)/(2)`

Decreasing rate is
`(1)/(3)` .

Using the exponential decay model:

`C(t)=C_0(1-r)^t`

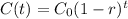
where,
`C_0` is initial amount of contaminants, r is the decreasing rate and t is time in hours.

Substituting the values, we get

`C(t)=(1)/(2)(1-(1)/(3))^t`

`C(t)=(1)/(2)((2)/(3))^t`

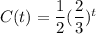
Therefore, the required function is
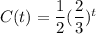`C(t)=(1)/(2)((2)/(3))^t`.