Answer:
The wavelength of these photons will become longer. The energy of each of these photons will become lower.
Step-by-step explanation:
Wavelength
Light can be considered as electromagnetic waves. The wavelength of a wave is equal to the minimum distance between two troughs (lowest points) in this wave. On the other hand, the frequency of a wave is equal to the number of wavelengths that this wave travels in unit time.
Assume that the speed of light stays the same. The distance that this beam of light travels in unit time will be the same. However, with a lower frequency, there would be fewer wavelengths in that same distance. Therefore, the size of each wavelength will become longer.
If
 represent the speed of light and
represent the speed of light and
 represents the frequency, then the wavelength would be:
represents the frequency, then the wavelength would be:
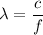 .
.
Energy
The energy
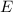 of each proton of a beam of light is proportional to the frequency
of each proton of a beam of light is proportional to the frequency
 of the light. Let
of the light. Let
 denote Planck's Constant. The numerical relation between
denote Planck's Constant. The numerical relation between
 and
and
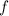 would be:
would be:
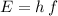 .
.
Therefore, if the frequency
 of this light becomes smaller, the energy
of this light becomes smaller, the energy
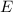 of each of its proton will also become proportionally lower.
of each of its proton will also become proportionally lower.