Question

Slope and y intercept of a line that passes through the points (-3,1) and (7,-5)?

Answer 1

The slope of the line is -3/5

The y-intercept of the line is 14/5

Explanation:

Equation of a line

A line can be completely defined by two points. Suppose we know the line passes through points A(x1,y1) and B(x2,y2).

The equation for a line can be written as:

`y=mx+b`

Where m is the slope and m is the y-intercept. Both values can be determined by using the coordinates of the given points.

First, determine the slope with the equation:

`\displaystyle m=(y_2-y_1)/(x_2-x_1)`

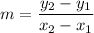
The points are: A(-3,1) B(7,-5)

`\displaystyle m=(-5-1)/(7-(-3))`

`\displaystyle m=(-6)/(7+3)=(-6)/(10)`

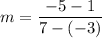
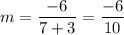
Simplifying by 2:

`\displaystyle m=-(3)/(5)`

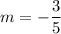
The slope of the line is -3/5

Using this value in the equation of the line:

`\displaystyle y=-(3)/(5)x+b`

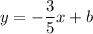
Use any of the given points to find b. Susbstituting point A(-3,1):

`\displaystyle 1=-(3)/(5)(-3)+b`

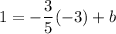
Operating:

`\displaystyle 1=-(9)/(5)+b`

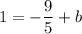
Moving the constants to the left side:

`\displaystyle 1+(9)/(5)=b\Rightarrow b=(14)/(5)`

`\boxed{\displaystyle b=(14)/(5)}`

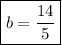
The y-intercept of the line is 14/5