Question

Find the general solution of the given differential equation.

x dy/ dx − y = x^2 sin(x)

Also determine whether there are any transient terms in the general solution. (Enter the transient terms as a comma-separated list; if there are none, enter NONE.)

Answer 1

`y=-x\,cos\,x+Cx`

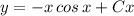
There are no transient terms.

Explanation:

Given:
`x\,(dy)/(dx) -y=x^2\,sin\,x`

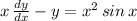
To find: general solution of the differential equation and the transient terms in the general solution.

Solution:

For an equation of the form
`(dy)/(dx)+yp(x)=q(x)`,

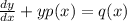solution is given by
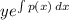`ye^{\int {p(x)} \, dx }` = ∫ q(x)
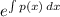`e^{\int {p(x)} \, dx }` dx

The given equation
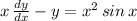`x\,(dy)/(dx) -y=x^2\,sin\,x` can be written as
`(dy)/(dx)-(y)/(x)=x\,sin\,x`

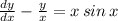
Here,

`p(x)=(-1)/(x)\,,\,q(x)=x\,sin\,x`

`e^{\int{p(x)} \, dx } =e^{\int{(-1)/(x) } \, dx } =e^(-ln(x)) =e^{ln(x^(-1) )}=x^(-1)=(1)/(x)`

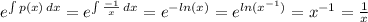
So,

the solution is
`(y)/(x)=\int (1)/(x)x\,sin\,x\,dx`

`(y)/(x) =\int\,sin\,x\,dx\\\\(y)/(x) =-cos\,x+C\\y=-x\,cos\,x+Cx`

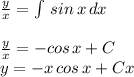
Here, C is a constant.

Transient term is a term such that it tends to 0 as x → ∞

Here, there does not exist any term that tends to 0 as x → ∞

So, there are no transient terms.