Answer:
Differential equation:
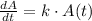 ,
,
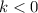 ,
,
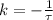 ,
,
 .
.
Solution:
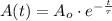
Explanation:
Let suppose that rate of change of the amount of Carbon-14 atoms are directly proportional to the current amount of Carbon-14 atoms. That is:
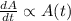
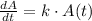
Where:
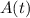 - Amount of Carbon-14 atoms, dimensionless.
- Amount of Carbon-14 atoms, dimensionless.
 - Proportionality constant, measured in
- Proportionality constant, measured in
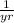 .
.
 must be negative as death rate is constant and birth rate is zero. (
must be negative as death rate is constant and birth rate is zero. (
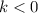 ). Dimensionally, we can rewritte this constant as following:
). Dimensionally, we can rewritte this constant as following:
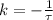
Where
 is the time constant (
is the time constant (
 ), measured in years.
), measured in years.
We can find the solution of the ordinary differential equation by separating each variable:
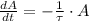
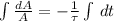
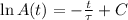
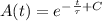

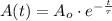
Where
 is the initial amount of atoms of Carbon-14.
is the initial amount of atoms of Carbon-14.