Question

Calculate the density of O2(g) at 415 K and 310 bar using the ideal gas and the van der Waals equations of state. Use a numerical solver to solve the van der Waals equation for Vm or use an iterative approach starting with Vm equal to the ideal gas result. Based on your result, does the attractive or repulsive contribution to the interaction potential dominate under these conditions?

Answer 1

Step-by-step explanation:

From the given information:

The density of O₂ gas =
`d_(ideal) = (P* M)/(RT)`

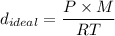
here:

P = pressure of the O₂ gas = 310 bar

=
`310 \ bar * (0.987 \ atm)/(1 \ bar)`

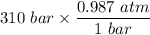
= 305.97 atm

The temperature T = 415 K

The rate R = 0.0821 L.atm/mol.K

molar mass of O₂ gas = 32 g/mol

∴

`d_(ideal) = (305.97 \ * 32)/(0.0821 * 415)`

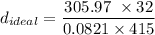
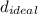`d_(ideal)` = 287.37 g/L

To find the density using the Van der Waal equation

Recall that:

the Van der Waal constant for O₂ is:

a = 1.382 bar. L²/mol² &

b = 0.0319 L/mol

The initial step is to determine the volume = Vm

The Van der Waal equation can be represented as:

`P =(RT)/(V-b)-(a)/(V^2)`

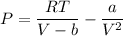
where;

R = gas constant (in bar) = 8.314 × 10⁻² L.bar/ K.mol

Replacing our values into the above equation, we have:

`310 =(0.08314* 415)/(V-0.0319)-(1.382)/(V^2)`

`310 =(34.5031)/(V-0.0319)-(1.382)/(V^2)`

`310V^3 -44.389V^2+1.382V-0.044=0`

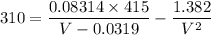
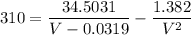
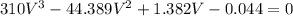
After solving;

V = 0.1152 L

∴

`d_(Van \ der \ Waal) = (32)/(0.1152)`

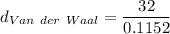
`d_(Van \ der \ Waal)` = 277.77 g/L

We say that the repulsive part of the interaction potential dominates because the results showcase that the density of the Van der Waals is lesser than the density of ideal gas.