Question

At a certain position in a piping system, a solution with a specific gravity of 1.50 passes through an 8-cm pipe with an average speed of 1.2 m/s. At some position downstream, the elevation of the pipe has increased 15.0 m and the pipe size has decreased to 5 cm. The temperature of the fluid is assumed constant at 30 C, and a heat loss of 25 Nm/kg occurs. Determine the change in pressure, in bars and megapascals.

Answer 1

`\Delta p=-2.60bar\\ \\\Delta p=-0.260MPa`

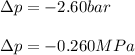
Step-by-step explanation:

Hello,

In this case, by using the Bernoulli equation:

`p_1+(1)/(2)\rho v^2_1+\rho gh_1= p_2+(1)/(2)\rho v^2_2+\rho gh_2+\rho h_L`

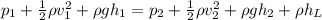
Whereas
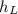`h_L` accounts for the heat loss, so we can compute the change of pressure by:

`p_1 +(1)/(2)\rho v^2_1+\rho gh_1= p_2+(1)/(2)\rho v^2_2+\rho gh_2+\rho h_L\\\\p_2-p_1=(1)/(2)\rho v^2_1+\rho gh_1-(1)/(2)\rho v^2_2-\rho gh_2-\rho h_L\\\\\Delta p=\rho *[(1)/(2)(v_1^2-v_2^2)+g(h_1-h_2)-h_L ]`

Thus, we must first compute the velocity inside the 5-cm section by using the continuity equation:

`v_2=v_1(A_1)/(A_2)=v_1*((\pi d_1^2/4)/(\pi d_2^2/4) ) \\\\v_2=1.2m/s*(8cm)/(5cm)=1.92m/s`

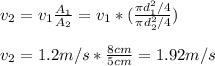
It means that the change in pressure in Pa turns out (density is 1500 kg/m³ given the specific gravity of the fluid):

`\Delta p=1500(kg)/(m^3) *[(1)/(2)((1.2(m)/(s))^2-(1.92(m)/(s))^2)+9.8m/s^2(0m-15.0m)-25(m^2)/(s^2) ]\\\\\Delta p=1500(kg)/(m^3)*(-1.1232(m^2)/(s^2) -147(m^2)/(s^2) -25(m^2)/(s^2) )\\\\\Delta p=-259684.8Pa`

Therefore, the change in pressure in bar and MPa turns out:

`\Delta p=-259684.8Pa*(1bar)/(1x10^5Pa)=-2.60bar\\ \\\Delta p=-259684.8Pa*(1MPa)/(1x10^6Pa)=-0.260MPa`

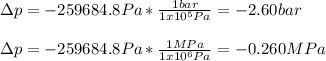
Such negative sign means that the pressure at the 5-cm section is lower than the pressure at the 8-cm section.

Best regards.