Question

Find a counterexample to disprove the conjecture.

Conjecture
AB
divides CAD into two angles. So, AB is an angle bisector of ZCAD.
m ZCAB = 20° andm ZDAB = 20°
m ZCAB = 20° andm ZCAD = 40°
m LDAB = 60° and m LCAD = 120°
mZCAB = 70° andm LDAB = 20°

Answer 1

f

Explanation:

Answer 2

D. mZCAB = 70° and mLDAB = 20°

Explanation:

An angle bisector is a line that divides a given angle into two equal parts. From the given question:

if angle CAD is divided into two unequal angles by AB, then AB is not an angle bisector of ZCAD.

For example: let mCAD =
`90^(o)`. Then if mCAB = mDAB =
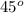`45^(o)`, then AB is an angle bisector.

But if mCAB
`\\eq` mDAB, then AB is not an angle bisector. Eg: mZCAB = 70° and mLDAB = 20°