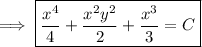Check if the equation is exact, which happens for ODEs of the form
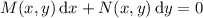
if
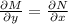 .
.
We have
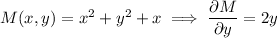
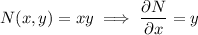
so the ODE is not quite exact, but we can find an integrating factor
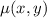 so that
so that
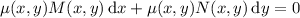
is exact, which would require
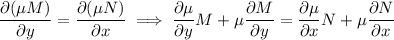
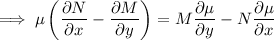
Notice that
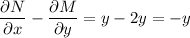
is independent of x, and dividing this by
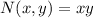 gives an expression independent of y. If we assume
gives an expression independent of y. If we assume
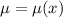 is a function of x alone, then
is a function of x alone, then
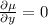 , and the partial differential equation above gives
, and the partial differential equation above gives
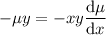
which is separable and we can solve for
 easily.
easily.
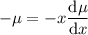
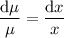
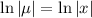
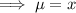
So, multiply the original ODE by x on both sides:
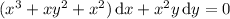
Now
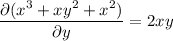
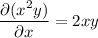
so the modified ODE is exact.
Now we look for a solution of the form
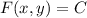 , with differential
, with differential
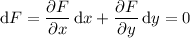
The solution F satisfies

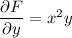
Integrating both sides of the first equation with respect to x gives
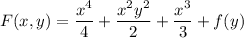
Differentiating both sides with respect to y gives
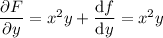
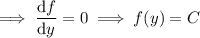
So the solution to the ODE is