Question

Equation of a circle that has a center of (-4,-1) and passes through (1,-3)

Answer 1

`(x + 4)^(2) + (y + 1)^(2) = 29`.

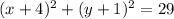Explanation:

The equation of a circle of radius
`r` and center
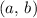`(a,\, b)` is:

`(x - a)^(2) + (y - b)^(2) = r^(2)`.

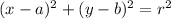In this question, it is given that the center is
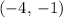`(-4,\, -1)`, such that
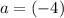`a = (-4)` while
`b = (-1)`.

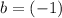The radius of this circle could be found as the distance between the center of this circle,
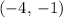`(-4,\, -1)`, and any point on the circle- such as
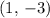`(1,\, -3)`. Using the distance formula, the radius of this circle would be:

`\begin{aligned}r &= \sqrt{((-4) - 1)^(2) + ((-1) - (-3))^(2)} \\ &= √(29)\end{aligned}`.

Therefore, the equation of this circle would be:

`(x - (-4))^(2) + (y - (-1))^(2) = (√(29))^(2)`.

Simplify to obtain:

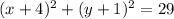`(x + 4)^(2) + (y + 1)^(2) = 29`.