Answer:
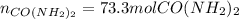
Step-by-step explanation:
Hello.
In this case, given the two balanced chemical reactions:
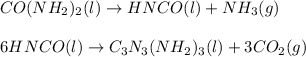
We first compute the moles of HNCO from the obtained 1.00 kg of melamine (molar mass 126 g/mol) by considering the 65 % yield:
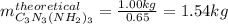
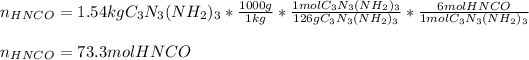
Next, we compute the moles of urea in the first chemical reaction:

Best regards.