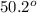Answer:
1. For quadrilateral ABCD:
AB = AD = 2.7, BC = DC = 3.2, and AC = 3.168
<BAC = <DAC
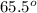 , <ABC = <ADC =
, <ABC = <ADC =
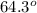 , and <ACB = <ACD =
, and <ACB = <ACD =
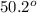
2. For quadrilateral ABCE:
AB = EC = 2.7, BC = AE = 3.2, and AC = 3.168
<BAC = <ACE
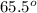 , <ABC = <AEC =
, <ABC = <AEC =
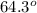 , and <ACB = <EAC =
, and <ACB = <EAC =
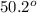
Explanation:
Applying the Cosine rule to triangle ABC,
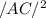 =
=
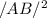 +
+
 - 2/AB/ x /BC/ Cos B
- 2/AB/ x /BC/ Cos B
=
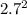 +
+
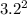 - 2 x 2.7 x 3.2 Cos 64.3
- 2 x 2.7 x 3.2 Cos 64.3
= 7.29 + 10.24 - 17.28 x 0.4337
= 17.53 - 7.49434
= 10.03566
AC =
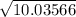
= 3.168
Applying the Sine rule,
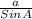 =
=
 =
=
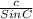
So that:
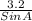 =
=
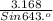
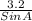 =
=

Sin A =
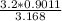
=
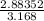
= 0.9102
⇒ A =
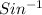 0.9102
0.9102
=
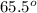
But sum of angles in a triangle is
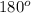 , so that;
, so that;
A + B + C =
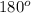
65.5 + 64.3 + C =
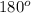
129.8 + C =
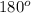
C =
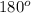 - 129.8
- 129.8
C =
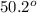
1. For quadrilateral ABCD:
AB = AD = 2.7, BC = DC = 3.2, and AC = 3.168
<BAC = <DAC
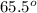 , <ABC = <ADC =
, <ABC = <ADC =
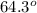 , and <ACB = <ACD =
, and <ACB = <ACD =
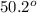
2. For quadrilateral ABCE:
AB = EC = 2.7, BC = AE = 3.2, and AC = 3.168
<BAC = <ACE
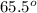 , <ABC = <AEC =
, <ABC = <AEC =
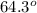 , and <ACB = <EAC =
, and <ACB = <EAC =