Answer:
C
Explanation:
Recall that the standard form for the explicit formula of a geometric sequence is given by:
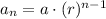
Where a is the initial term, r is the common ratio, and n is the nth term.
Our sequence is 8, 4, 2, 1, and so on.
Hence, our initial term a is 8.
Each subsequent term is half of the previous one. So, our common ratio r is 1/2.
Therefore, by substitution, we acquire:
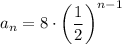
In conclusion, our answer is C.