Question

Im giving 100 Points to anyone who could solve this for me please.

In the segment below, segment DC = 29,

Answer 1

AB = 27.2

BC = 33.5

AC = 50.4

∠A = 38°

∠ABC = 112°

Explanation:

Trigonometric ratios

`\sf \sin(\theta)=(O)/(H)\quad\cos(\theta)=(A)/(H)\quad\tan(\theta)=(O)/(A)`

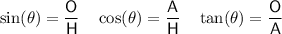
where:

• 
  `\theta` is the angle
• O is the side opposite the angle
• A is the side adjacent the angle
• H is the hypotenuse (the side opposite the right angle)

`\implies \sf \cos(30^(\circ))=(29)/(BC)`

`\implies \sf BC=(29)/(\cos(30^(\circ)))`

`\implies \sf BC=(58√(3))/(3)=33.5\:(nearest\:tenth)`

`\implies \sf \tan(30^(\circ))=(BD)/(29)`

`\implies \sf BD=29\tan(30^(\circ))`

`\implies \sf BD=(29√(3))/(3)`

`\implies \sf \sin(38^(\circ))=(BD)/(AB)`

`\implies \sf AB=((29√(3))/(3))/(\sin(38^(\circ)))`

`\implies \sf AB=27.2\:(nearest\:tenth)`

`\implies \sf \tan(38^(\circ))=(BD)/(AD)`

`\implies \sf AD=((29√(3))/(3))/(\tan(38^(\circ)))`

`\implies \sf AD=21.4\:(nearest\:tenth)`

`\implies \sf AC=AD+DC=21.4+29=50.4`

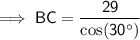
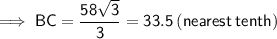
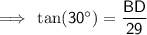
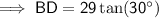
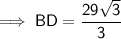
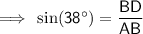
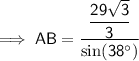
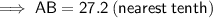
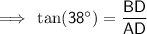
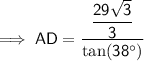
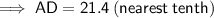
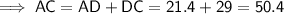
The interior angles of a triangle sum to 180°

⇒ ∠A + 52° + 90° = 180°

⇒ ∠A = 180° - 90° - 52°

⇒ ∠A = 38°

⇒ ∠ABC + 38° + 30° = 180°

⇒ ∠ABC = 180° - 38° - 30°

⇒ ∠ABC = 112°

**I have checked the measures using a graphing programme - see attached**