Answer:
Option (2)
Explanation:
Formula to determine the final amount of an element after t years is,
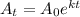
where
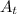 = Final amount
= Final amount
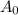 = Initial amount
= Initial amount
t = Duration or time
k = decay constant
If the half life period of a C-14 isotope = 5730 years
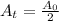 [For half life period]
[For half life period]
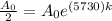
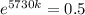
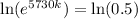
0.5730k = -0.6931
k =
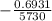 = -0.000121
= -0.000121
Therefore, formula for the radioactive decay will be.
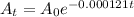
Option (2) will be the answer.