Question

The function in the table is linear.

a. Determine the slope of the function. Show your work.
b. Write an equation for the function. Use function notation. Show your work.

Answer 1

a. The slope of the function is 3.

b. The equation of the function in function notation is y = 3(x + 1) - 8.

The slope of the function can be calculated as follows:

Slope = (Change in y) / (Change in x)

In this case, the change in y is 1 - (-8) = 9 and the change in x is 2 - (-1) = 3. Therefore, the slope of the function is 9 / 3 = 3.

To write an equation for the function in function notation, we can use the point-slope form of linear equations:

`y - y_1 = m(x - x_1)`

where m is the slope of the line and
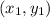`(x_1, y_1)` is a point on the line.

We can choose the point (-1, -8) as our point on the line. Substituting the slope and point into the equation above, we get:

y - (-8) = 3(x - (-1))

Simplifying the equation, we get:

y + 8 = 3(x + 1)

y = 3(x + 1) - 8

y = 3x- 5

This is the equation of the function in function notation.

Answer 2

Explanation:

Function given by the table represents a linear function.

a). Since, slope of a linear function passing through two points
`(x_1,y_1)` and
`(x_2,y_2)` is,

Slope =
`(y_2-y_1)/(x_2-x_1)`

Slope of the linear function passing through two points (0, -5) and (2, 1) will be,

Slope =
`(1+5)/(2-0)=3`

b). Let the equation of the function is,

y = mx + b

Where m = slope of the function

b = y-intercept

Here slope of the function 'm' = 3

y-intercept of he function = -5 [y-value of the function at x = 0]

Therefore, the function is,

y = 3x - 5