Question

The angle whose measure is (3pi)/4 terminates in quadrant || and its reference angle is for pi/4. what are the reciprocal trigonometric function values for (3pi)/4? check all that apply.

sec((3pi)/4) = - 1/2
sec((3pi)/4) = - sqrt(2)
csc((3pi)/4) = - sqrt(2)
cot ((3pi) /4 )=-1
csc((3pi)/4) = sqrt(2)

Answer 1

Options (2), (4) and (5)

Explanation:

An angle whose measure is
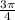`(3\pi )/(4)` terminates in quadrant 2 and its reference angle is
`(\pi)/(4)`.

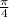As we know only Sine value of a reference angle which terminates in 2nd quadrant is positive. Tan and Cosine of this angle are negative.

Similarly, Cosec of a reference angle terminating in 2nd quadrant is positive while sec and cot values of the same angle are negative in the 2nd quadrant.

`\text{Cosec}((3\pi)/(4))=\text{Cosec}((\pi)/(4))=√(2)`

`\text{Sec}(3\pi)/(4)=-\text{Sec}(\pi)/(4)=-√(2)`

`\text{Cot}((3\pi)/(4))=-\text{Cot}((\pi)/(4) )=-1`

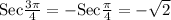
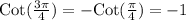
Therefore, Options (2), (4) and (5) will be the answer.