Question

Consider a rectangle that has a perimeter of
`80\ \text{cm}`. Write a function
`A(l)` that represents the area of the rectangle with length
`l`.

Answer 1

`A(L) =40L-L^2`

Explanation:

The perimeter of a rectangle is modeled by the function:
`P = 2L + 2W`

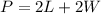
You are given that the perimeter is 80 cm, so substitute this value in for
`P`

• 
  `80=2L+2W`

You want the function
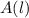`A(l)` to represent the area of the rectangle in terms of the length
`L`, so, therefore, you want to solve for the width of the rectangle (so you can still have that
`L` variable).

Solve for
`W` by first subtracting
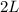`2L` from both sides of the equation.

• 
  `80-2L = 2W`

Then divide both sides of the equation by 2 to isolate the variable
`W`.

• 
  `(80-2L)/(2)=W`

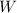This can be simplified even further:

• 
  `W=40-L`

The area of a rectangle is modeled by the function:
`A=LW`

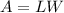
You have already solved for
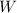`W`, so substitute
`40-L` for it.

• 
  `A=L(40-L)`

Use the distributive property to multiply everything inside the parentheses by
`L`.

• 
  `A=40L-L^2`

Since this function is in terms of
`L`, you can write:

• 
  `A(L) =40L-L^2`

This function represents the area of the rectangle with a perimeter of 80 cm and length
`L`.

Answer 2

`\boxed{A(l)= 40l - l^2}`

Explanation:

We know that a rectangle has four sides - two lengths and two widths. We also know that the lengths are equal and that the widths are equal. Therefore, to find the perimeter of a rectangle, we use:

`P = 2L + 2W`

However, this problem asks to find the area of the rectangle. The area can be found by multiplying length and width (A = L × W).

Using our formula above, we can solve for the length.

`80 = 2L + 2W` (divide everything by 2)

`40 = L + W` (subtract W in order to solve for L)

`40 - L = W` (rearrange W to the left - standard equation notation)

`W = 40 - L`

The area of a rectangle is solved using the formula A = LW, so we just need to input our values and solve for A.

`A(l) = (40 - l)(l)` (distribute the W throughout)

`A(l)= 40l - l^2`

This is your final function. Hope this helps!