Answer:
See below for answers and explanations (with attached graph)
Explanation:
It helps to transform the equation into vertex form by completing the square because it tells us a lot about the characteristics of the parabola:
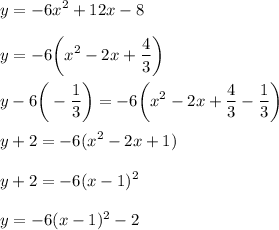
Since vertex form is
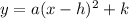 , we identify the vertex to be
, we identify the vertex to be
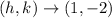 and the axis of symmetry to be
and the axis of symmetry to be
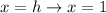 . The y-intercept can be found by setting
. The y-intercept can be found by setting
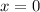 and evaluating:
and evaluating:
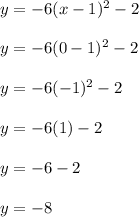
Hence, the y-intercept of the parabola is
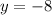 , or
, or
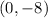 as an ordered pair.
as an ordered pair.