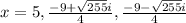Answer:
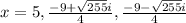
Explanation:
1) Move all terms to one side.
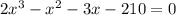
2) Factor
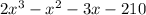 using Polynomial Division.
using Polynomial Division.
1 - Factor the following.
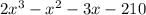
2 - First, find all factors of the constant term 210.
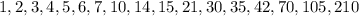
3) Try each factor above using the Remainder Theorem.
Substitute 1 into x. Since the result is not 0, x-1 is not a factor..
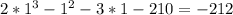
Substitute -1 into x. Since the result is not 0, x+1 is not a factor..
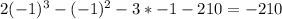
Substitute 2 into x. Since the result is not 0, x-2 is not a factor..
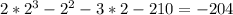
Substitute -2 into x. Since the result is not 0, x+2 is not a factor..
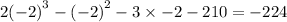
Substitute 3 into x. Since the result is not 0, x-3 is not a factor..
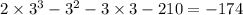
Substitute -3 into x. Since the result is not 0, x+3 is not a factor..
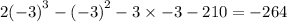
Substitute 5 into x. Since the result is 0, x-5 is a factor..
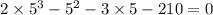
------------------------------------------------------------------------------------------
⇒
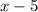
4) Polynomial Division: Divide
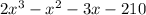 by
by
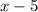 .
.
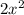
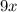
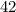
-------------------------------------------------------------------------
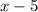 |
|
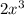
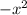
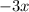
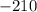
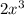
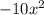
-----------------------------------------------------------------------
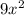
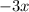
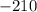
--------------------------------------------------------------------------
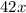
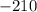
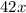
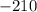
-------------------------------------------------------------------------
5) Rewrite the expression using the above.
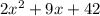
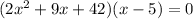
3) Solve for
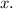
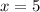
4) Use the Quadratic Formula.
1 - In general, given
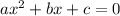 , there exists two solutions where:
, there exists two solutions where:
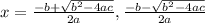
2 - In this case,
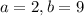 and
and
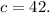
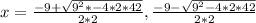
3 - Simplify.
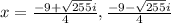
5) Collect all solutions from the previous steps.