Answer:
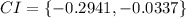
Explanation:
Assuming conditions are met, the formula for a confidence interval (CI) for the difference between two population proportions is
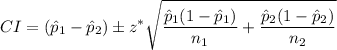 where
where
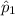 and
and
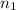 are the sample proportion and sample size of the first sample, and
are the sample proportion and sample size of the first sample, and
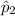 and
and
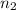 are the sample proportion and sample size of the second sample.
are the sample proportion and sample size of the second sample.
We see that
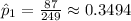 and
and
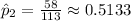 . We also know that a 98% confidence level corresponds to a critical value of
. We also know that a 98% confidence level corresponds to a critical value of
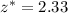 , so we can plug these values into the formula to get our desired confidence interval:
, so we can plug these values into the formula to get our desired confidence interval:
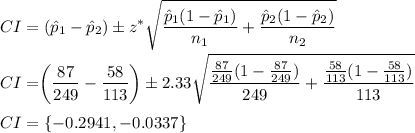
Hence, we are 98% confident that the true difference in the proportion of people that live in a city who identify as a democrat and the proportion of people that live in a rural area who identify as a democrat is contained within the interval {-0.2941,-0.0337}
The 98% confidence interval also suggests that it may be more likely that identified democrats in a rural area have a greater proportion than identified democrats in a city since the differences in the interval are less than 0.