Question

A fully-loaded Boeing 747 accelerates on the ground at 1.8 m/s2. How much runway does it need, in meters, to achieve a liftoff velocity of 82 m/s?

Answer 1

runway length = 1,867.78 meters

Step-by-step explanation:

This problem can be solved using equation of motion

`v^2 = u^2 + \ 2as`

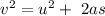
where

v is the final velocity

u is the initial velocity and

s is the distance a body moved to reach speed equal to final velocity .

__________________________________

Given

a = 1.8 m/s2

u is the initial velocity which will be zero as the plane starts on the ground at that point speed is zero

Let S be the distance taken to reach speed 82 m/s at acceleration of 1.8 m/s^2

This , distance will be the length of runway as well.

v = 82 m/s

using the equation of motion

`v^2 = u^2 + \ 2as\\=> 82^2 = 0^2 + \ 2*1.8*S\\=> 6724 = 0 + 3.6 S\\=> S = 6724/3.6 = 1,867. 78`

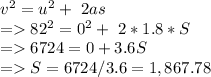
Thus, distance is 1,867.78 meters,

Hence , we can say that runway length should be 1,867.78 meters so that when plane lifts off its speed is 82 m/s.