Question

Find the value of y​

Answer 1

Hello!!! Princess Sakura here ^^

Explanation:

First you should find out what x is and to do that you should do...

`5x-38=3x-4`

Tip: You should know that those angles are alternate interior and alternate interior angles are equal to each other.

So anyways when you go and solve it you should get...

`5x-38=3x-4\\2x-38=-4\\2x=34\\x=17`

so know that you know what x is I strongly recommend that you plug it in for

`5x-38` because you will need it soon.

`5x-38\\5(17)-38\\85-38\\47`

Great now that we know the measure of that angle we can finally go and find y.

We can do that by solving for this equation...

`7y-20+47+90=180`

Tip: The sum of all the angles in the triangle is 180.

`7y-20+47+90=180\\7y+117= 180\\7y= 63\\y=9`

So now we are finally done the value of y is 9.

Answer 2

`y=9`

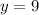
Explanation:

First, let's find the value of x.

Note that the two equations with the x are alternate interior angles. Therefore, their angle measures are equivalent. So, we can write the following equation:

`5x-38=3x-4`

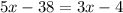
Solve for x. Let's add 38 to both sides:

`5x=3x+34`

Subtract 3x from both sides:

`2x=34`

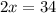
Divide both sides by 2. So, the value of x is:

`x=17`

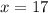
We can see that we have a right triangle.

The sum of the three interior angles of a triangle is always 180. Therefore, we can write that:

`90+(7y-20)+(5x-38)=90`

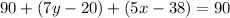
Since we already know that x is 17, substitute 17 for x. This yields:

`90+(7y-20)+(5(17)-38)=180`

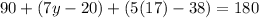
Now, we can solve for y. Multiply:

`90+(7y-20)+(85-38)=180`

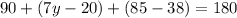
Combine like terms:

`(7y)+(90-20+85-38)=180`

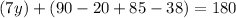
Evaluate:

`7y+117=180`

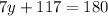
Subtract 117 from both sides:

`7y=63`

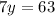
Divide both sides by 7. So, the value of y is:

`y=9`

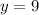
And we're done!