Question

A car travels 100 m while decelerating to 8 m/s in 5 s.
a) What was its initial speed?

Answer 1

Vi = 32 [m/s]

Step-by-step explanation:

In order to solve this problem we must use the following the two following kinematics equations.

`v_(f) =v_(i) - (a*t)\\`

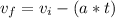
The negative sign of the second term of the equation means that the velocity decreases, as indicated in the problem.

where:

Vf = final velocity = 8[m/s]

Vi = initial velocity [m/s]

a = acceleration = [m/s^2]

t = time = 5 [s]

Now replacing:

8 = Vi - 5*a

Vi = (8 + 5*a)

As we can see we have two unknowns the initial velocity and the acceleration, so we must use a second kinematics equation.

`v_(f)^(2) = v_(i)^(2) - (2*a*d)`

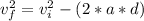
where:

d = distance = 100[m]

(8^2) = (8 + 5*a)^2 - (2*a*100)

64 = (64 + 80*a + 25*a^2) - 200*a

0 = 80*a - 200*a + 25*a^2

0 = - 120*a + 25*a^2

0 = 25*a(a - 4.8)

therefore:

a = 0 or a = 4.8 [m/s^2]

We choose the value of 4.8 as the acceleration value, since the zero value would not apply.

Returning to the first equation:

8 = Vi - (4.8*5)

Vi = 32 [m/s]