Question

A1 = 10 and an =an -1 +2

Answer 1

I assume you're asking to solve for the n-th term in the sequence,
`a_n`.

From the given recursive rule,

`a_n = a_(n-1) + 2 \implies a_(n-1) = a_(n-2) + 2`

and by substitution,

`\implies a_n = a_(n-2) + 2*2`

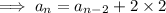
Similarly,

`a_n = a_(n-1) + 2 \implies a_(n-2) = a_(n-3) + 2`

`\implies a_n = a_(n-3) + 3*2`

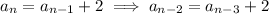
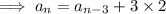
The pattern continues, so that we can write the n-th term in terms of the 1st one:

`a_n = a_1 + (n-1)*2 \implies a_n = 10 + 2(n-1) = \boxed{2n+8}`

So the first few terms of the sequence are

{10, 12, 14, 16, 18, 20, …}