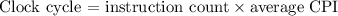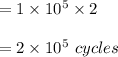Question

Consider two different implementations of the same instruction set architecture. The instructions can be divided into four classes according to their CPI (class A, B, C and D). P1 with a clock rate of 3GHz and CPIs of 3, 2, 1, 4, and P2 with a clock rate of 2.5GHz and CPIs of 2, 2, 2, 2.Processor Class A Class B Class C Class DP1 3 2 1 4P2 2 2 2 2Given a program with a dynamic instruction count of 1.0E5 instructions divided into classes as follows: 10% class A, 30% class B, 40% class C, and 20% class D.1. Which implementation is faster?2. What is the global CPI for each implementation?3. Find the clock cycles required in both cases?

Answer 1

Follows are the solution to this question:

Step-by-step explanation:

The architecture of two separate iterations with the same the instruction set can be defined in the attached file please find it.

Calculating the value of total instruction count:

`= 1 * 10^(5) \\\\= 10^5`

`\text{P1 clock rate} = 3 \ GHz \\ \\\text{P2 clock rate} = 2.5 \ GHz \\\\\text{Class Division: 10 \% of class A,} \text{30 \% of class B, 40 \% of class C, 20 \% of class D} \\\\`

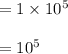
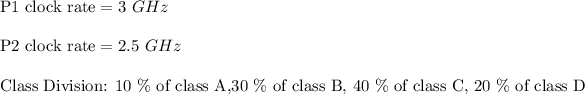
In point a:

Calculating P1 device mean CPI:

`Average CPI = (summation * instruction \ count * CPI)/(total \ instruction \ count)\\`

`= (10^5 * 10 \% * 3 + 10^5 * 30 \% * 2 + 10^5 * 40 \% * 2 + 10^5 * 20%`
`* 4) * \frac{1} {1 * 10^5}\\\\`

`= ((3 * 10^4 + 6 * 10^4 + 8 * 10^4 + 8 * 10^4))/(1 * 10^5)\\\\ = (25* 10^4)/(1 * 10^5)\\\\= 2.5`

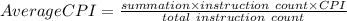
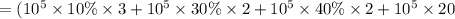
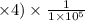
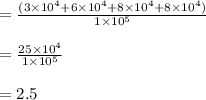
Estimating P2 device Average CPI:

`= (1 * 10^5 * 10 \% *2 + 1 * 10^5 * 30 \% * 2 + 1 * 10^5 * 40 \% * 2 + 1 * 10^5 * 20 \%`
`* 2) * (1)/( 1 * 10^5)`

`= ((2 * 10^4 + 6 * 10^4 + 8 * 10^4 + 4 * 10^4))/(1 * 10^5) \\\\= (20 * 10^4)/(1 * 10^5) \\\\= 2 \\`

`\text{Execution time} = \frac{\text{instruction count} * \text{average CPI}}{clock rate}}`

`= (1 * 10^5 * 2.5)/(3) \ GHz \\\\ = (1 * 10^5 * 2.5)/(3 * 10^9) \ sec \ as \ 1 \ GHz \\\\ = 10^9 \ Hz \\\\= 0.083 \ msec \ as \ 1 \ sec \\\\ = 10^3 \ msec`

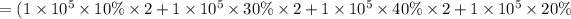
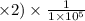
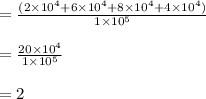
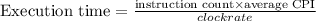
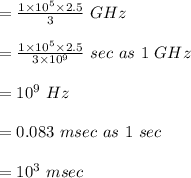
Calculating processor execution time P2:

`= (1 * 10^5 * 2)/(2.5) \ GHz \\\\= (1 * 10^5 * 2)/(2.5 * 10^9) \ sec \ as\ 1 \ GHz \ = 10^9 \ Hz \\\\ = 0.080 \ msec \ as \ 1 \ sec \\\\ = 10^3 \ msec`

Since P2 is less than P1 for processor execution time, P2 is therefore faster than P1.

In point b:

Global processor P1 CPI = 2.5

Global processor P2 CPI = 2

In point c:

Finding Processor P1 clock cycles:

`\text{Clock cycle = instruction count} * \text{average CPI}`

`= 1 * 10^5 * 2.5 \\\\ = 2.5 * 10^5 \ cycles`

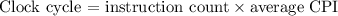
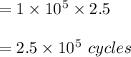
Finding Processor P2 clock cycles:

`\text{Clock cycle = instruction count} * \text{average CPI} \\\\`

`= 1 * 10^(5) * 2\\\\ = 2 * 10^(5) \ cycles\\\\`