Question

Six months ago you won $1,000,000 on a scratch-off lottery ticket and invested your winnings with a financial advisor at the investment firm Dewey, Lie, and Howe. The earnings on the investment are compounded monthly.You complain to the financial advisor that your returns after 6 months are inadequate and do not even cover the advisor's fees. The 6 monthly interest rates (in decimal form) have been R1 = -0.4, R2= 0.67, R3 = 1.0, R4 = -0.5, R5 = 0.2, R6 = -0.165.1. What is the total worth of your investment after 6 months?$The financial advisor responds that you shouldn't complain because the average return over the 6 months has been an impressive 13.4% (0.134 in decimal form). You angrily respond that the average return is not representative of the 6-month investment performance, and that the geometric mean should be used instead.2. What is the geometric mean of the above monthly returns? (express as a decimal; round off to 3 decimal places)geometric mean

Answer 1

The total worth of the investment after 6 months is T = $ 1004004

The geometric mean of the above monthly returns is
`\= G = 0.001`

Explanation:

From the question we are told that

The growth for each month are

R1 = -0.4, R2= 0.67, R3 = 1.0, R4 = -0.5, R5 = 0.2, R6 = -0.165

The amount invested is
`A = \$ 1,000,000`

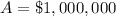
The number period of the investment is 6 months

Generally the worth of the investment after each month is

`G_i = G_p * (1 + R_i)`

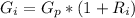
Here
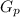`G_p` is the worth of the investment the previous year

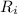`R_i` is the growth for that month

So considering the first month

`G_1 = G_p (1 + R_1)`

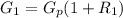
Here
`G_p = A`

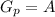
So

`G_1 = 1000000 (1 -0.4)`

`G_1 = 600000`

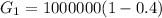
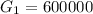
Considering the second month

Here
`G_p = 600000`

So

`G_2 = 600000 (1 + 0.67)`

=>
`G_2 = 1002000`

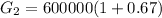
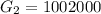
Considering the third month

Here
`G_p = 1002000`

So

`G_3 = 1002000 (1 + 1)`

`G_3 = 2004000`

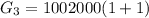
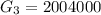
Considering the fourth month

Here
`G_p = 2004000`

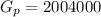
So

`G_4= 2004000 (1 + -0.5)`

`G_4= 1002000`

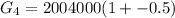
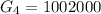
Considering the fifth month

Here
`G_p = 1002000`

So

`G_5= 1002000 (1 + 0.2)`

`G_5= 1202400`

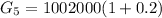
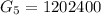
Considering the six month

Here
`G_p = 1202400`

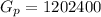
So

`G_6= 1202400 (1 -0.165)`

`G_6= 1004004`

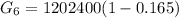
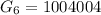
Generally the total worth of the investment after 6 months is T = $ 1004004

Generally the geometric mean of the monthly returns is

`\= G = \sqrt[n]{ [(1 + R_1 ) * \cdots (1 + R_n)} ]-1`

Here n represents the number of months which has a value n = 6

So

`\= G = \sqrt[6]{[(1+ (-0.4 )) * (1 + 0.67) * \cdots * (1 + (-0.165))]} - 1`

`\= G = 0.001`