Answer:
The value is

Explanation:
From the question we are told that
The total number of cards is

Let k represent the winnings and loss when any card is drawn
So k = $5 when a faced card is drawn
So k= $ 20 when an Ace card is drawn
So g = - $2 when any other card is drawn
Generally in a standard deck of card
The number of Ace is 4
The number of queen is 4
The number of jack is 4
Therefore the number off faced cards is
R = 4 + 4 + 4 = 12
Generally the number of other cards is
Y = n - R
=> Y = 52 - 12
=> Y = 36
Generally the probability of drawing a faced card is mathematically represented as
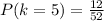
Generally the probability of drawing a Ace card is mathematically represented as
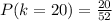
Generally the probability of drawing a other card is mathematically represented as
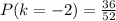
Generally the expected profit from any one draw is mathematically represented as
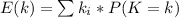
=>
![E(k) = 5 * ( 12)/(52) + 20( 20)/(52) + [- 2 * ( 36)/(52)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/q71rfs1l19uzl9koqdydekv0exl4tx6cwy.png)
=>
